為了獲得毫焦量級(jí)的脈沖能量和數(shù)個(gè)吉瓦的峰值功率���,摻鐿光纖放大系統(tǒng)通常使用極大模場(chǎng)直徑(MFD)的增益光纖并結(jié)合啁啾脈沖放大(CPA)技術(shù)��。進(jìn)一步提升脈沖能量和峰值功率依賴(lài)于近些年發(fā)展的相干合成技術(shù)��。
分脈沖放大(Divided-pulse amplification����, DPA)是一種常用的相干合成技術(shù):在 DPA 系統(tǒng)中���,通過(guò)在放大前將初始脈沖等分成時(shí)域上分離的子脈沖串�,以降低脈沖在放大時(shí)的峰值功率���;子脈沖串經(jīng)過(guò)放大之后重新合成為一個(gè)脈沖�����。DPA 的相干合成效率主要受到三方面的限制:(1)增益飽和導(dǎo)致子脈沖間的強(qiáng)度差異�;(2)非線(xiàn)性效應(yīng)將子脈沖間的強(qiáng)度差異轉(zhuǎn)化為相位差異����;(3)器件缺陷�。本文介紹的兩篇文獻(xiàn)均對(duì)啁啾脈沖-分脈沖放大系統(tǒng)(CPA-DPA)進(jìn)行了詳細(xì)的數(shù)值模擬����,并重點(diǎn)研究了合成效率與增益飽和的關(guān)系。
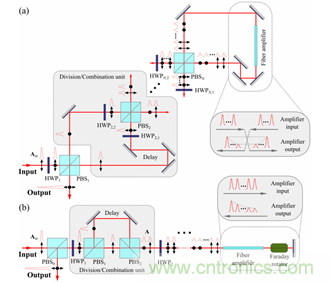
圖 1 (a) Sagnac 型 DPA 裝置和 (b) 雙通 DPA 裝置的示意圖
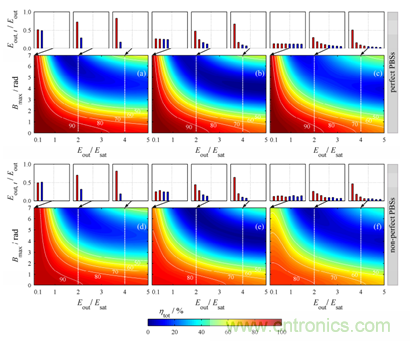
2013 年��,Marco Kienel 等人探究了兩種 CPA-DPA 系統(tǒng)合成效率的影響因素[1]��。第一種(圖 1a)是 Sagnac 裝置����,其脈沖在時(shí)間與空間上均被等分,雙向通過(guò)增益光纖放大后合成�。第二種(圖 1b)是雙通裝置,等分的子脈沖序列來(lái)回兩次通過(guò)增益光纖放大并合成����。圖 2 顯示了雙通 DPA 裝置的合成效率與增益飽和,非線(xiàn)性強(qiáng)度和 PBS 對(duì)比度的關(guān)系�。圖 2(a,d)�, (b,e)���, (c����,f)分別代表分脈沖數(shù)量為 2,4��,8 的情況����。其中����,(a-c)對(duì)應(yīng)理想的 PBS,而(d-f)對(duì)應(yīng)對(duì)比度有缺陷的 PBS���。圖像橫軸為輸出能量 Eout 與飽和能量 Esat 的比值����,代表增益飽和效應(yīng)的強(qiáng)度�����,縱軸是單個(gè)子脈沖累積的最大 B 積分�,表征系統(tǒng)的非線(xiàn)性強(qiáng)度。
如圖 2(a)所示�����,當(dāng)不存在非線(xiàn)性效應(yīng)(Bmax = 0)時(shí),僅增益飽和增強(qiáng)即可造成雙脈沖合成效率下降��,因?yàn)樵鲆骘柡徒o予了兩個(gè)子脈沖強(qiáng)度上的差異����,導(dǎo)致合成偏振態(tài)偏轉(zhuǎn),使脈沖在通過(guò)輸出端 PBS 時(shí)損失能量�。而當(dāng)非線(xiàn)性效應(yīng)存在時(shí),強(qiáng)度相關(guān)的非線(xiàn)性相移會(huì)把增益飽和造成的強(qiáng)度差異轉(zhuǎn)化為相位差異��,極大地?fù)p害合成的線(xiàn)偏振程度����,進(jìn)一步降低合成效率。除非增益飽和很弱�,兩脈沖的強(qiáng)度差異小,即使 Bmax 很大��,兩脈沖 B 積分差依然不大����,合成效率仍維持較高水平。更多分脈沖數(shù)量(圖 2(b,c))與 PBS 缺陷(圖 2(d-f))的情況整體與理想 PBS 的雙脈沖(圖 2(a))類(lèi)似�����,只是合成效率更加敏感�����,因?yàn)槎啻魏铣稍黾恿讼到y(tǒng)的復(fù)雜度��,PBS 缺陷引入了更多不規(guī)則的子脈沖強(qiáng)度差�����。
圖 2 雙通 DPA 系統(tǒng)中總合成效率與增益飽和���,非線(xiàn)性強(qiáng)度,PBS 缺陷的關(guān)系
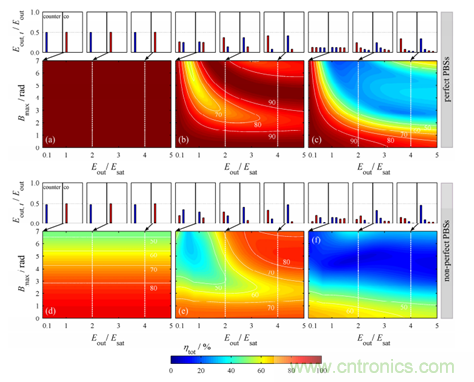
相較于雙通裝置�����,Sagnac 裝置的合成效率隨上述物理因素的變化規(guī)律略有不同�。當(dāng)分脈沖數(shù)量為 2 時(shí)(圖 3(a)),兩強(qiáng)度相同但正交的子脈沖通過(guò)環(huán)路相向傳輸�����,經(jīng)歷完全相同的增益和非線(xiàn)性相移,合成效率為 100%���。而在四個(gè)子脈沖的情況下(圖 3 (b))���,Sagnac 裝置的合成效率亦遠(yuǎn)高于雙通的 DPA 系統(tǒng)。這是因?yàn)?Sagnac 裝置結(jié)構(gòu)對(duì)稱(chēng)���,4 脈沖的第一次合成始終是完美的��,減少的合成效率僅是第二次合成中兩脈沖相位差所致合成線(xiàn)偏振度的降低�����。
當(dāng)分脈沖數(shù)量增加至 8 時(shí)(圖 3(c))��,合成效率才降到與雙通系統(tǒng)類(lèi)似的水平�����。此外����,相較于雙通的 DPA 系統(tǒng),PBS 缺陷(圖 3(d-f))會(huì)破壞 Sagnac 裝置的對(duì)稱(chēng)性�,因而對(duì)合成效率有更嚴(yán)重的影響。
圖 3 Sagnac DPA 系統(tǒng)中總合成效率與增益飽和�����,非線(xiàn)性強(qiáng)度����,PBS 缺陷的關(guān)系
除了上述物理效應(yīng),還有一些其他的效應(yīng)可能會(huì)降低合成效率���,例如源于 Kramers-Kr?nig 關(guān)系的相移,增益飽和對(duì)脈沖的整形作用���,和分脈沖相互重合導(dǎo)致的交叉相位調(diào)制(XPM)��。
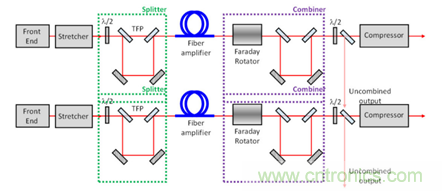
因此����,在 2016 年����,F(xiàn). GUICHARD 等人對(duì) CPA-DPA 系統(tǒng)進(jìn)行了更嚴(yán)格且詳細(xì)的仿真,計(jì)算了包括 XPM、增益飽和與 K-K 關(guān)系的耦合非線(xiàn)性薛定諤方程[2]�。作者所考慮的是如圖 4 所示的雙通摻鐿 CPA-DPA 系統(tǒng)。上半部分的合成器件與分脈沖器件的參數(shù)保持完全相同����,為被動(dòng)系統(tǒng);下半部分的合成器件與分脈沖器件的參數(shù)可獨(dú)立調(diào)節(jié)�,但需通過(guò)掃描最大輸出功率以確定合成器件的參數(shù),為主動(dòng)系統(tǒng)�����。
圖 4 被動(dòng)與主動(dòng)的雙通 CPA-DPA 系統(tǒng)
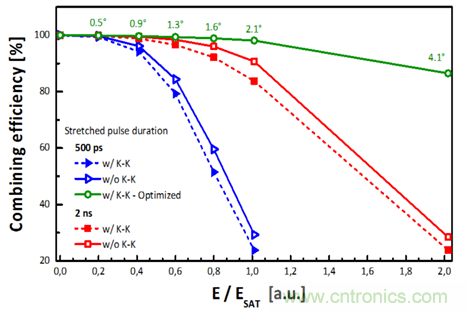
具有 2 個(gè)子脈沖的被動(dòng) DPA 系統(tǒng)的合成效率模擬結(jié)果如圖 5 所示�����。理論上��,由于增益飽和的影響���,第一子脈沖的增益高于第二子脈沖���,輸出時(shí),強(qiáng)度的差異會(huì)略微降低合成效率��。而自相位調(diào)制(SPM)和 K-K 相移又會(huì)將兩脈沖的強(qiáng)度差轉(zhuǎn)化為相差,進(jìn)一步造成合成效率的降低�。為了區(qū)分這些效應(yīng)之間的貢獻(xiàn),作者首先討論了不同非線(xiàn)性強(qiáng)度的模擬結(jié)果:將輸入脈沖展寬至 500 ps(藍(lán)線(xiàn))或 2 ns(紅線(xiàn))��,對(duì)應(yīng)每個(gè)子脈沖的平均 B 積分分別為 12 rad 和 3 rad(E / Esat = 1 時(shí))�����,在輸出能量接近飽和能量���,增益飽和效應(yīng)增強(qiáng)時(shí)����,很明顯非線(xiàn)性強(qiáng)的情況(藍(lán)線(xiàn))合成效率下降得更快����。其次��,從忽略 K-K 關(guān)系后再模擬的結(jié)果可知(虛線(xiàn))�,SPM 是兩脈沖相差的主要貢獻(xiàn)者,K-K 關(guān)系對(duì)合成效率的降低只占少部分����。
圖 5 具有 2 個(gè)子脈沖的被動(dòng) DPA 系統(tǒng)的合成效率與增益飽和的關(guān)系
作者還試圖通過(guò)旋轉(zhuǎn)分脈沖器件與合成器件的半波片角度來(lái)改變子脈沖放大前的能量分配��,以補(bǔ)償增益飽和導(dǎo)致的強(qiáng)度差異�����。模擬結(jié)果如圖 5 綠線(xiàn)所示��,作者成功的優(yōu)化了合成效率并顯示了每個(gè)輸出能量對(duì)應(yīng)旋轉(zhuǎn)的最佳角度�。它清楚地表明�����,調(diào)節(jié)半波片是將有效相干合成區(qū)域拓展至放大器飽和能量之外的有效方法���。
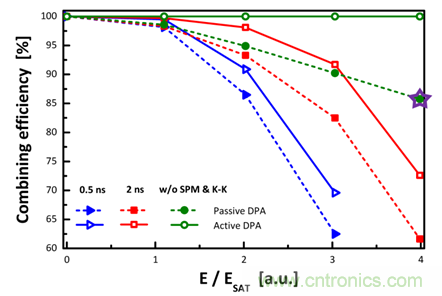
圖 6 展示了分脈沖數(shù)量為 4 的 DPA 系統(tǒng)的模擬結(jié)果����。其中的藍(lán)線(xiàn)��,紅線(xiàn)�����,綠線(xiàn)分別對(duì)應(yīng)高非線(xiàn)性強(qiáng)度�,低非線(xiàn)性強(qiáng)度和無(wú)非線(xiàn)性效應(yīng)三種情況���。虛線(xiàn)代表被動(dòng) DPA 系統(tǒng),而實(shí)線(xiàn)代表主動(dòng) DPA 系統(tǒng)�。所有曲線(xiàn)所代表的合成效率都已通過(guò)旋轉(zhuǎn)半波片的角度盡可能地優(yōu)化了。藍(lán)線(xiàn)和紅線(xiàn)的變化趨勢(shì)與圖 5 類(lèi)似�,再次說(shuō)明非線(xiàn)性越強(qiáng),增益飽和對(duì)合成效率的影響越大�。
值得注意的是,在輸出能量的值接近飽和能量四倍的情況下(每個(gè)子脈沖能量都與飽和能量相當(dāng))��,盡管沒(méi)有 SPM 和 KK 關(guān)系引入子脈沖間的相差�����,合成效率也會(huì)因過(guò)強(qiáng)的增益飽和而顯著降低���,且被動(dòng) DPA 系統(tǒng)不能補(bǔ)償這種由純粹強(qiáng)度失衡導(dǎo)致的低合成效率(圖 6 綠色虛線(xiàn))����。但是�����,強(qiáng)度差異引起的合成效率降低可以通過(guò)主動(dòng)的 DPA 系統(tǒng)完美解決(圖 6 綠色實(shí)線(xiàn)):先獨(dú)立調(diào)節(jié)輸入端的半波片角度�����,使輸入脈沖分為能量前低后高的子脈沖序列�,以補(bǔ)償增益飽和給放大后子脈沖帶來(lái)的能量差,這樣獲得的相等幅度的放大子脈沖��,再通過(guò)獨(dú)立調(diào)節(jié)輸出端半波片的角度來(lái)完美合成����,從而產(chǎn)生極高的合成效率。除此以外�����,增加分脈沖數(shù)量也是優(yōu)化合成效率的常用方法��,其不僅能降低每個(gè)子脈沖的峰值功率��,從而降低非線(xiàn)性的強(qiáng)度�,還可以減弱增益飽和對(duì)脈沖造成的影響。
圖 6 具有 4 個(gè)子脈沖的被動(dòng)和主動(dòng) DPA 系統(tǒng)的合成效率與增益飽和的關(guān)系
綜上所述����,兩篇文章均通過(guò)模擬描述了增益飽和影響 DPA 合成的機(jī)制,為實(shí)驗(yàn)中觀察到的接近飽和能量時(shí)的合成效率下降提供了可靠的解釋與解決的方案��。雖然兩篇文章均提出了采用主動(dòng) DPA 設(shè)計(jì),增加分脈沖數(shù)量的優(yōu)化方法�����,但由于當(dāng)前系統(tǒng)缺乏對(duì)每個(gè)子脈沖強(qiáng)度和相位的控制手段���,任意縮放分脈沖數(shù)量并不可行����。未來(lái)可以考慮使用響應(yīng)足夠快的電/聲光調(diào)制器之類(lèi)的元件來(lái)控制每個(gè)子脈沖的強(qiáng)度和相位����,以解決此問(wèn)題。