【導讀】將并聯(lián)和串聯(lián)設計混合在一起的一種有趣的電路,是與輸出負載串聯(lián)的并聯(lián)LC濾波器電路,下面我們將其稱為(L // C)-R電路。下面的圖1給出了這種架構的表示:
本文介紹利用并聯(lián)L // C而引起的諧振現(xiàn)象,并利用該現(xiàn)象我們對電子中的濾波器模塊進行設計。
帶阻濾波器
將并聯(lián)和串聯(lián)設計混合在一起的一種有趣的電路,是與輸出負載串聯(lián)的并聯(lián)LC濾波器電路,下面我們將其稱為(L // C)-R電路。下面的圖1給出了這種架構的表示:
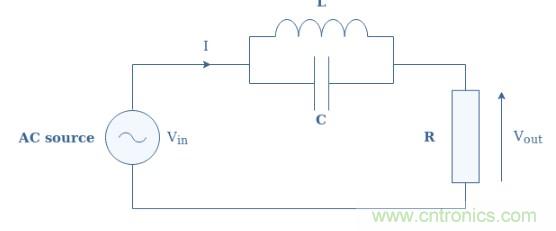
圖1:(L // C)-R電路圖
如果我們將Z L // C稱為并聯(lián)LC結構的阻抗,則可以寫成V in = V out + Z L // C ×I。知道I = V out / R并通過用V out分解表達式,我們可以在幾步之后寫出(L // C)-R電路的傳遞函數(shù):
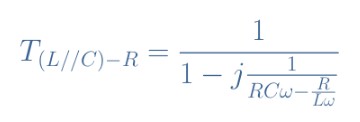
eq 2:(L // C)-R傳遞函數(shù)
我們假設L = 3 mH,C = 5 nF,R = 10kΩ和20kΩ,我們來分析該電路的傳遞函數(shù),
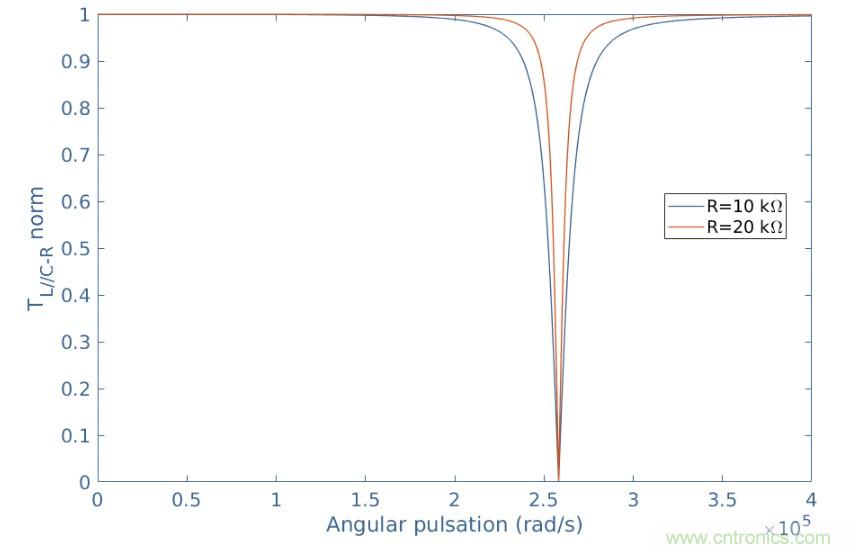
圖2:(L // C)-R傳遞函數(shù)的圖
圖2陳述了這樣的一個事實,即當電阻增加時,該帶阻濾波器的帶寬Δω變窄,這是因為Q 串聯(lián) =(1 / R)√( L / C)=ω 0 /Δω。
實際上,該定義對并聯(lián)電路無效,并聯(lián)結構的公式變?yōu)镼 并聯(lián) = 1 / Q series =R√(C / L),這解釋了先前確定的圖1中的現(xiàn)象。
實際上,并聯(lián)RLC電路的特征參數(shù)是串聯(lián)RLC電路的倒數(shù)。
帶通濾波器
一個有趣的概念稱為對偶性,使我們能夠從另一電路的知識中直接找到新電路的方式?;谶@樣的事實推論,可以將應用于電流或電壓的方程式應用于特定結構。
讓我們更清楚一點,再考慮一下上面詳細介紹的帶阻濾波器示例。我們將這種配置稱為(L // C)-R,因為L//C電路與電阻R串聯(lián)(-)。我們已經(jīng)看到該電路充當該電壓的帶阻濾波器。
該電路的對偶電路是圖3中所示的(L // R)// R電路:
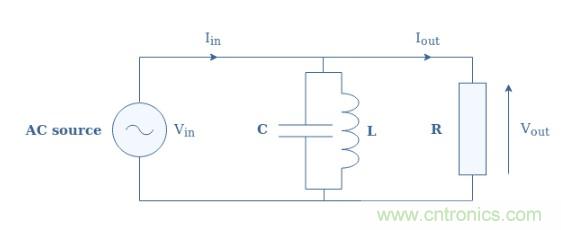
圖3:圖1的對偶結構
對偶性概念告訴我們,該對偶電路是帶阻濾波器(即帶通濾波器)的對偶。為了驗證該假設,我們可以通過寫成I in = I out + Y L // C ×V out來開始,這與上一節(jié)中顯示的等式相同,但適用于電流,如對偶性概念所述。ÿ L// C是L // C的導納和等于1 / Z L// C。
知道V out = R×I out并通過用I out分解表達式,得出:
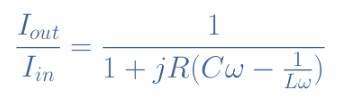
eq 3:(L // C)// R傳遞函數(shù)
我們可以看到,等式3與等式2非常相似,但是虛數(shù)項是相反的,這決定了了帶通濾波器的行為。我們可以再次考慮相同的值L = 3 mH,C = 5 nF和R = 10kΩ和20kΩ,并繪制此傳遞函數(shù),以得出本節(jié)的結論并確認帶通濾波器:
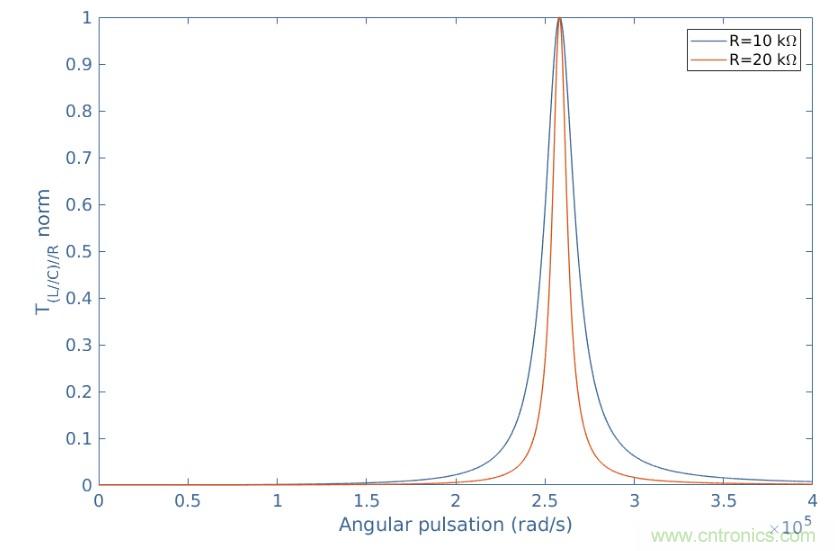
圖4:(L // C)// R傳遞函數(shù)圖
結論
并聯(lián)RLC電路的行為與串聯(lián)結構完全不同。這是由于L // C電路的能量相互交換的現(xiàn)象,稱為共振。
這種現(xiàn)象是由于互連的電感器和電容器之間發(fā)生了相互放電/電荷。這樣的電路的阻抗理論上趨于無窮大值在特定的脈動ω 0稱為共振脈動(對于f或共振頻率0)。在實際電路中,此阻抗會由于內部電阻行為而達到峰值。
推薦閱讀:








