【導(dǎo)讀】最近一時沖動，買了一個成本非常低的電子骰子套件。組裝的過程還是挺有古典趣味的。這個電路的設(shè)計風(fēng)格還停留在70年代：一個CD4017，一個NE555，一對晶體管。當(dāng)然，我開始思考，怎樣用最高效的方式來實現(xiàn)呢？當(dāng)然這意味著需要用到微控制器；而且還要達(dá)到我們資源利用盡可能低的目標(biāo)。那么用一個帶有3個I/O口的ATtiny10能夠?qū)崿F(xiàn)嗎？
骰子的圖案包含7個LED，但是，你可能很快就發(fā)現(xiàn)其中六個LED都是成對亮滅的，所以我們就具有3對LED外加一個額外的LED需要控制。這需要四個I/O口——但還是太多了！
要減少需要的I/O口，一個很顯然的使用方法是“查理復(fù)用技術(shù)（Charliplexing）”，你能在網(wǎng)上找到很多關(guān)于查理復(fù)用技術(shù)電子骰子的電路圖。簡單來說，查理復(fù)用技術(shù)允許使用n個I/O口控制n²-n個LED。所以當(dāng)我們采用查理復(fù)用技術(shù)時，我們就需要三個I/O口就夠了。但對于我們使用的ATtiny10來說還是太多了，因為我們還需要一個額外的I/O口來“搖骰子”。
查理復(fù)用技術(shù)使用了微控制器I/O引腳的三態(tài)特性。同時激活的只有兩個I/O口——其中一個為高電平，另一個為低電平——而其他引腳就是高阻抗?fàn)顟B(tài)。只有以正確的極性和激活的引腳直接相連的LED才能發(fā)光。而不與引腳直接相連的路徑上的LED——比如連接到激活引腳的的是兩個串聯(lián)的LED——那么這些LED就不會發(fā)光，這是因為二極管的非線性電流-電壓特性導(dǎo)致的。
現(xiàn)在，你可能會疑惑當(dāng)只有一個I/O口（而不是兩個）激活時會發(fā)生什么了？在查理復(fù)用技術(shù)的方案中什么也不會發(fā)生，但我們可以利用這一點。
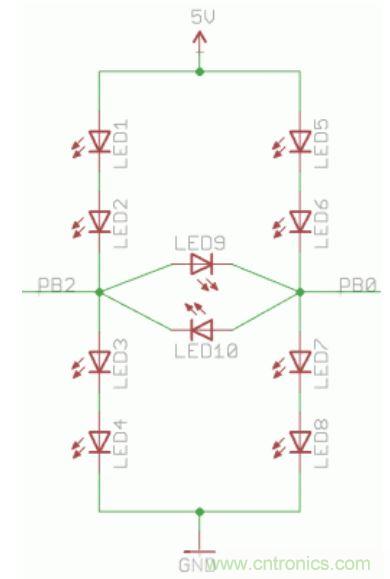
以上的電路展示了怎樣以不同的方案連接LED。除了兩個I/O引腳之間的反平行對之外，作為查理復(fù)用技術(shù)的使用習(xí)慣，LED還需要連接到VCC（5V）和GND。串聯(lián)的四個LED（LED1-4與LED5-8）的正向電壓之和超過5V，所以當(dāng)PB0和PB2處于高阻抗（Z）狀態(tài)時，這些燈都不會發(fā)光。
當(dāng)PB0和PB2中有一個引腳處于高電平或低電平狀態(tài)，而另一個引腳為高阻抗?fàn)顟B(tài)時，那就會有一對LED會發(fā)光。而當(dāng)PB0為高電平而PB2為低電平或恰好相反時，LED9或LED10就將和一對LED并聯(lián)。這時大部分的電流會流過單個LED，所以這時只有LED9或LED10會發(fā)光。
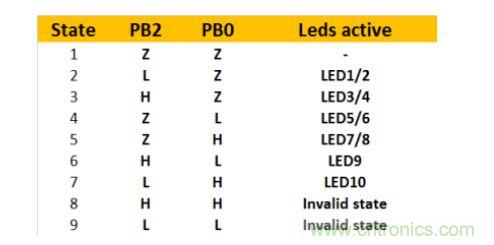
上表是可能的編碼?？吹搅藛?？兩個引腳可以控制六個部分的LED！這正是我們所需要的，任務(wù)完成了。
但需要說明一點：單個LED的亮度并不同于串聯(lián)的兩個LED。這可能需要在查理復(fù)用技術(shù)中進行校正。但是事實上由于人眼對光亮度的差異并沒有特別敏感，兩者的差異只能說是勉強可見。
[page]
簡單測試一下（LED并未像骰子一樣排列）?？雌饋砦覀冃碌亩鄰?fù)用技術(shù)能很好地工作。注意一點，該電路需要由AVR I/O接口的內(nèi)部阻抗。這確實有效，但是在“真正”的設(shè)計中應(yīng)當(dāng)避免。
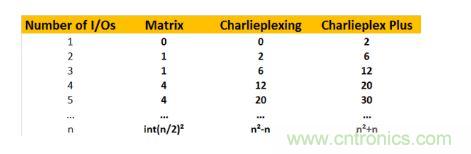
我們可以講這種新的方案成為“查理復(fù)用+（Charlieplex Plus）”。分析表明，依靠這樣的技術(shù)，一個I/O口可以比普通的查理復(fù)用技術(shù)多控制兩個LED。也就是說n個I/O口所能控制的LED數(shù)量就為2n+n²-n = n²+n。具體情況如上表所示。
你應(yīng)該在你的設(shè)計中采用這種思路嗎？恐怕不應(yīng)該，因為這種做法的缺陷和限制甚至比現(xiàn)有的查理復(fù)用還多。但是這卻很有趣！
所以回到最初，控制電子骰子最少需要多少個I/O口呢？
答案是2.
